군집분석
- 거리 기반 모델
- 비지도 학습(Y 없음)
- 여러 변수를 사용하여 각 데이터들끼리의 유사도를 거리로 측정하여 유사성이 높은 데이터들끼리 하나의 군집으로 묶는 과정
- 거리를 사용하여 유사성을 측정
** 주의
1) 이상치에 민감
2) 스케일링에 민감
3) 변수 조합에 영향을 많이 받음
4) 변수의 형태에 영향을 많이 받음(범주형 보다는 수치형이 유리)
명목형일 때에는 일치도로 거리를 계산, 즉 변수의 형태에 영향을 받는다는 의미
1. 종류
1) 계층형 군집 분석
- 거리가 가장 가까운 데이터들끼리 순차적으로 그룹을 형성하는 과정(항상 동일한 결과 리턴)
- 군집의 수가 정해져 있지 않아도 수행 가능
- 군집과의 거리를 정의해야 함(single, complete, average, centroid, ward 등)
2) 비계층적 군집 분석
- 군집의 수 만큼 랜덤하게 초기 seed값 할당
- seed로부터 거리가 가장 가까운 데이터들끼리 순차적으로 그룹을 형성하는 과정
이전 군집분석 모형은, 군집을 두 개로 나눈다면 두 개의 seed가 필요한데, 전혀 데이터와 상관없는 중심으로 데이터가 가지고 있는 분포를 측정하여 범위 안에 아무 점이나 두 점을 찍어 가까운 데이터들을 묶어나가는 과정이었다면, 최근 군집분석 모형은 데이터 포인트 내에서 대표자를 만들어 군집 분석의 seed 할당 과정이 달라짐. 랜덤하게 초기 seed값을 할당하기 때문
3) 혼합 분포 군집
- 모든 데이터들이 군집의 수만큼 특정 분포를 따른다는 가정
정규분포에서 왔다면, 두 모수는 평균과 분산. 두 모수를 가지고 데이터 포인트가 분포에 있을 확률이 높다고 가정. 최소 제곱법과는 다르게 확률을 높인다 하여(=우도를 높인다) 최대 우도 추정법이라고 함
- 최대우도추정법에 의해 군집을 결정
4) DBSCAN
- 데이터포인트끼리 가까운 거리의 군집을 형성하는 과정이 아님
- 데이터포인트끼리 갖는 분포적 특성을 반영하여 군집을 형성 → 단순히 선형적으로 군집을 형성하는 게 아닌, 기하학적으로 군집 형성이 가능
- 반경 내 min_sample에 데이터가 존재할 경우만 군집을 형성
- 반경(ε)과 min_sample(하나의 서브 군집을 형성하는 최소 기준이 되는 데이터 수)에 따라 결과가 많이 달라짐
- 군집의 수를 정하지 않아도 됨
5) SOM
2. 평가 **(목적: 알고리즘 비교, 군집의 수 비교, 두 관점으로 군집분석을 평가하여야 함)
- 적절한 군집의 수 결정
- 서로 다른 군집 무형 비교 시(계층 VS. 비계층)
분류분석처럼 y가 있으면 accuracy 구하고, 회귀분석처럼 y가 있으면 오차라는 것을 측정하여 평가를 할 수 있음. 즉, loss function을 정의할 수 있음
하지만 연관분석이나 군집분석은 y가 없기 때문에 y로 인한 평가 matric이 존재하지 않음
1) 총분산의 분해: BETWEEN_SS / TOTAL_SS로 군집을 평가
TOTAL_SS : 편차 제곱합(총분산)
TOTAL_SS = WITHIN_SS + BETWEEN_SS
(총분산) (군집내 분산) (군집간 분산)
(그룹내 분산) (그룹간 분산)
좋은 군집일수록 그룹간 분산이 커짐.
2) 실루엣 계수
** 개별 실루엣 계수
- 각 데이터포인트 마다의 실루엣 계수
- -1~1범위 내
- 높을 수록 해당 데이터 포인트가 잘 군집화 되어 있다는 의미
실제로는 개벌 실루엣 계수를 보지는 않음
** 전체 실루엣 계수
- 개별 실루엣 계수의 평균
- 0~1 범위 내
- 클 수록 좋은 군집
a = 각 데이터 포인트와 같은 군집 내에 있는 다른 데이터 포인트들과의 거리의 평균(군집 내 유사도)
b = 각 데이터 포인트와 다른 군집 중 가장 가까운 군집 내에 있는 데이터 포인트들과의 거리의 평균(군집 간 유사도, 이질성)
s = (b - a) / max(a, b)
3) Dunn index(DI)
- 변동량(거리)에 초점을 맞춘 평가 지표
- DI가 클 수록 좋은 군집
- DI = 군집간 거리 중 최소값 / 군집내 거리 중 최대값
위의 1)~3)이 삼총사임. 서로 비슷한 결과가 도출됨
예제 - iris data를 사용하여 설명변수만을 사용하여 군집분석 수행(비계층적 군집분석)
1. 데이터 로딩

2. 스케일링

3. 비계층적 군집분석 수행

R은 아직까지 k-means++ 버전이 아님. 초기값 할당하는 방법에 있어 버전이 다름. 파이썬에서는 kmeans++라고 해서 초기 seed값을 기존 관측치로부터 생성

비슷하게 나누어 진 듯 하다.
4. 군집 평가
1) 변동량 기준

0행은 첫 번째 그룹에 대한 각 설명변수 평균
1행은 두 번째 그룹에 대한 각 설명변수 평균
2행은 세 번째 그룹에 대한 각 설명변수 평균
즉, 그룹에 대한 평균을 구할 수 있음.
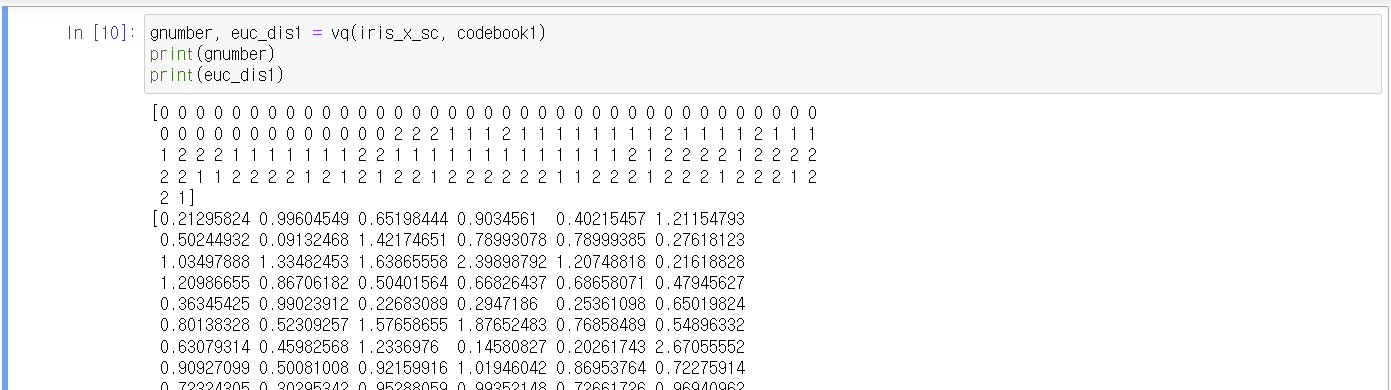
그룹넘버와 각각에 대한 within_ss를 구해줌

2) 실루엣 계수
개별 실루엣 계수

전체 실루엣 계수

5. 적절한 군집의 수 구하기

그래프 시각화(군집의 수의 변화에 따른 평가점수의 변동)

k가 증가하면 witin_ss가 작아짐. 반대로 between_ss가 커짐
적절한 군집의 수를 결정하기 위하여 이런 평가지표를 쓰는 것이지만 k가 커질수록 between_ss도 계속 올라갈 수밖에 없음.
그러므로 최대값을 갖는 k값을 찾으면 안됨. elbow point를 찾아야 함.
3일 때가 변동폭이 높음
5라는 포인트도 개선의 여지가 있겠음.
우리가 iris 클러스터 개수를 몰랐다면 3~5의 군집을 고려했을 것임.
예제 - iris data를 사용하여 설명변수만을 사용하여 군집분석 수행 (SOM 군집분석)
1. 데이터 로딩

2. 스케일링

3. SOM 모델링
pip install sklearn_som
SOM(m = 3, # 격자 크기
n = 3, # 격자 크기(mxn = unit의 수)
dim = 3, # input layer unit 수 → 설명변수의 수에 맞게
lr = 1, # learning rate(학습률). 학습률이 크면 너무 rough하게 업데이트 되어서 속도는 빨라지나,
최적화 과정에 예측력이 떨어짐. 반대로 업데이트를 너무 빈번하게 하게 되면 속도가
느려짐. 이런 것들을 튜닝하여야 함.
max_iter = 3000, # 반복 수
random_state = 0) # seed

4. 평가
1) 변동량

2) 실루엣 계수

'배우기 > 복습노트[Python과 분석]' 카테고리의 다른 글
| [복습] Python | 분석 | 시계열 분석(2) (0) | 2024.03.10 |
|---|---|
| [복습] Python | 분석 | 군집분석(5) (0) | 2024.03.06 |
| [복습] Python | 분석 | 회귀분석(2) - (전통)회귀분석 총정리 + 하루끝(20240215) (0) | 2024.03.04 |
| [복습] Python | 분석 | 연관분석(2) (0) | 2024.03.04 |
| [복습] Python | 분석 | 연관분석(1) + 하루끝(20240214) (0) | 2024.02.14 |



