1. 데이터 로딩

2. EDA(Exploratory Data Anlaysis)
1) corr


corr은 음의 값이 커져도 값이 유의미해지므로 절대값을 씌워서 해석해보는 것도 좋음.
다만 절대값을 씌우면 음의 상관관계는 알 수 없음에 주의할 것.
2) 분포 시각화 → 스케일링 고려가 필요한지 분포 시각화로 확인

pd에서 제공해주는 scatter는 dataframe을 받는다.
자기 자신에 대한 상관계수는 1이므로, 자기 자신에 대한 분포가 출력된다(대각선).
time 변수가 정규성에 위배되어보이기는 하나, 문제가 되지는 않을 듯 하다.
회귀분석에서 선형성, 등분산성, 독립성, 정규성 등은 잔차의 정규성을 따라야 한다.
그런데 time은 잔차에 대한 그래프가 아니므로 문제가 되지 않는 것이다.
변수 분포를 보는 이유: 스케일링 고려가 필요할 수도 있기 때문(로그 스케일링 같은)
x들이 수치형이기 때문에 스케일링이 필요한지 확인하기 위해 분포를 확인하였다.
3. 모델링


모델의 유의성 검정
- R스퀘어가 높아도 모형 유의성이 높지 않으면 소용이 없겠음(모형이 유의하지 않으면 R스퀘어도 높게 나오지는 않음)
- F-test결과가 0.05보다 작기 때문에 모형이 유의하지 않다는 영가설 기각(유의수준 0.05 기준)
- 모형이 유의하지 않다는 영가설을 기각하여 모형이 유의할 것으로 판단
회귀계수 각각의 유의성 검정
- 변수의 p-value가 작기 때문에 pressure, time 변수가 유의한 것으로 확인됨.
- temperature는 유의수준보다 크기 때문에 영가설 채택. 즉, temperature 회귀계수가 0일 것이라는 영가설 채택.
따라서 temperature는 유의하지 않을 것으로 확인됨
- 그러나 많은 연구에 따르면 철의 강도는 온도의 영향을 받을 것으로 예상하고 있음. 따라서 이 점을 고려하여 여러 변수 연구를 수행한 결과 temperature와 pressure 과 서로 연관되어서 y변수에 영향을 줄 것으로 기대됨( 두 변수의 교호 작용이 유의미할 것으로 기대됨)
4. 진단
1) 모형 유의성 검정: 영가설 기각 → 모형 유의
모형 유의성 검정 결과 영가설 기가되어 모형이 유의한 것으로 판단됨
2) 회귀 계수 유의성 검정: Temperature 변수만 영가설 채택 → temperature 유의하지 않음. 나머지 변수 모두 유의.
그램에도 불구하고 결정계수는 높았음
3) 결정계수 / 수정 결정 계수 : 0.874 / 0.859
interaction impact에 대한 효과를 넣으면 결정계수가 올라갈 것으로 기대됨.
5. VIF(분산 팽창 지수)
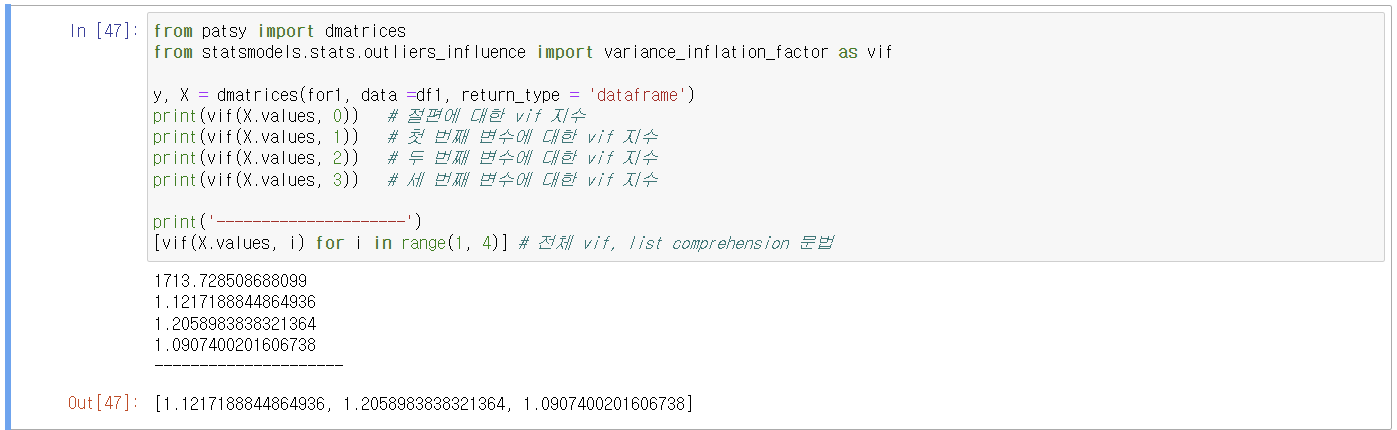
다중공선성의 문제는 발견되지 않음.
6. 교호 작용 효과 검증
의심스러운 두 변수에 대해서만 수행: TemperatureXPressure

interaction에 대한 문제점: 스케일링을 해야 함. 더 큰 수치를 가지고 있는 값이 더 크게 반영되므로.
스케일링 수행

스케일링을 위해 데이터 복사
1) Standard Scaling 후 회귀 모형 생성

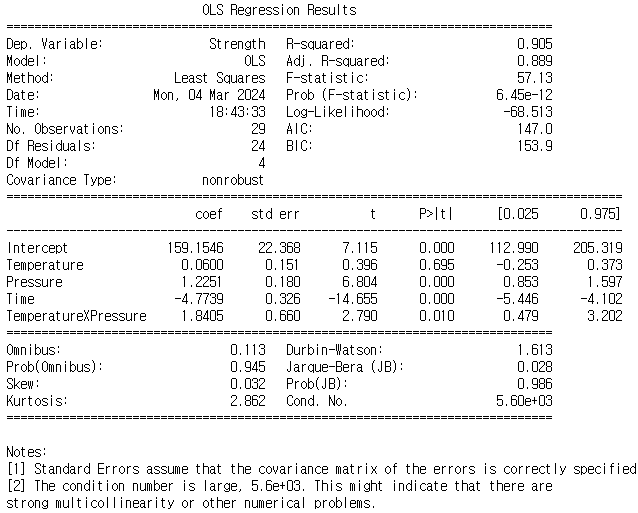
변수가 추가됐기 때문에 결정계수는 올라갔을 것임. 그러므로 수정 결정계수를 확인하여야 함.
수정된 R스퀘어가 0.3점이나 오름. 꽤 큰 변화임.
TemperatureXPressure의 p-value가 0.05보다 작으므로 유의한 것으로 나타남.
TemperatureXPressure의 interaction effect의 효과가 있을 것으로 확인됨.
문제는 temperature가 여전히 유의하지 않다고 출력됨. 그래서 temperature를 제거하고 고려하여야 함.
Temperature 제거 후 회귀 모델링

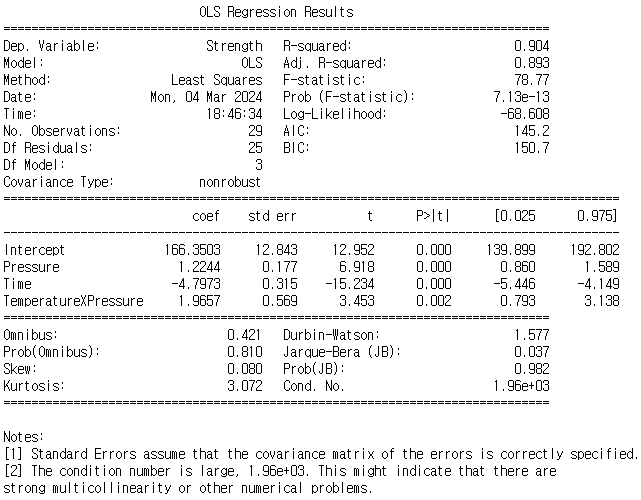
거의 90점에 가까운 점수를 보임(수정된 R스퀘어)
어떤 변수도 이 모형에 위배가 된다라고 판단되지 않음
2) MinMax Scaling 후 회귀 모형 생성


수정된 R스퀘어가 오르긴 함.
여기서 Pressure의 p-value를 보면 삭제해야 할 것처럼 나타남.
하지만 그렇다고 하여 temperature와 pressure를 한꺼번에 지워서는 안됨. 변수 분석을 수행하여야 함
유효했던 pressure는 유지하고 먼저 temperature부터 삭제해보는 것이 좋음.
계수 크기로는 temperature가 더 효과가 좋은 것으로 보이기는 함.
Temperature 제거 후 회귀 모델링

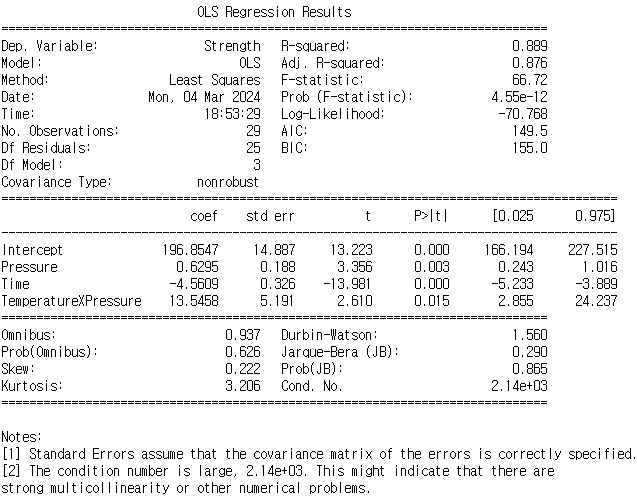
제거 했을 때 수정된 R스퀘어가 더 떨어진 것으로 나타남.
pressure는 다시 유의한 것으로 보임.
모든 변수가 다 유의한 형태로 출력됨.
스케일링 결과 Standard Scaler 효과가 더 큰 것으로 확인됨.
스케일링 없이 만든 교호작용 효과

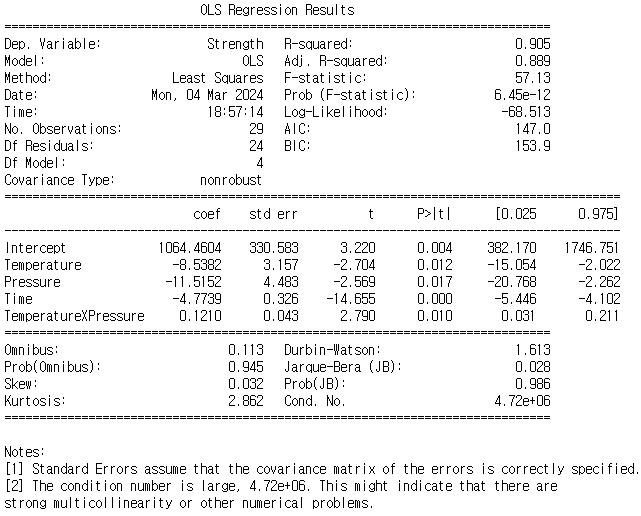
Temperature, Pressure 둘 다 유의한 것으로 나타남. 그래서 주의하여야 한다. 이대로 믿어서는 안됨.
스케일링 필수.
기존 산점도에서도 Temperature는 단독 효과가 없을 것으로 나타나긴 했었음.
회귀분석에서는 분류분석보다 교호작용이 더 자주 등장한다.
수많은 변수 중에 의미 있는 interaction을 찾기도 어렵다.
알지 못하는 경우가 많을 때에는 일일이 확인해보아야 한다.
스케일링에 대한 변화도 있기 때문에 꼭 확인할 것.
최종 모델에 대한 진단.
7. 모형 가정 진단(최종 모형에 대한 진단 → m22, Temperature 제거하고, StandardScaler 한 모델링)
1) 선형성: 종속변수와 독립변수가 관계가 있는지 확인하는 것
종속변수와 독립변수의 산점도
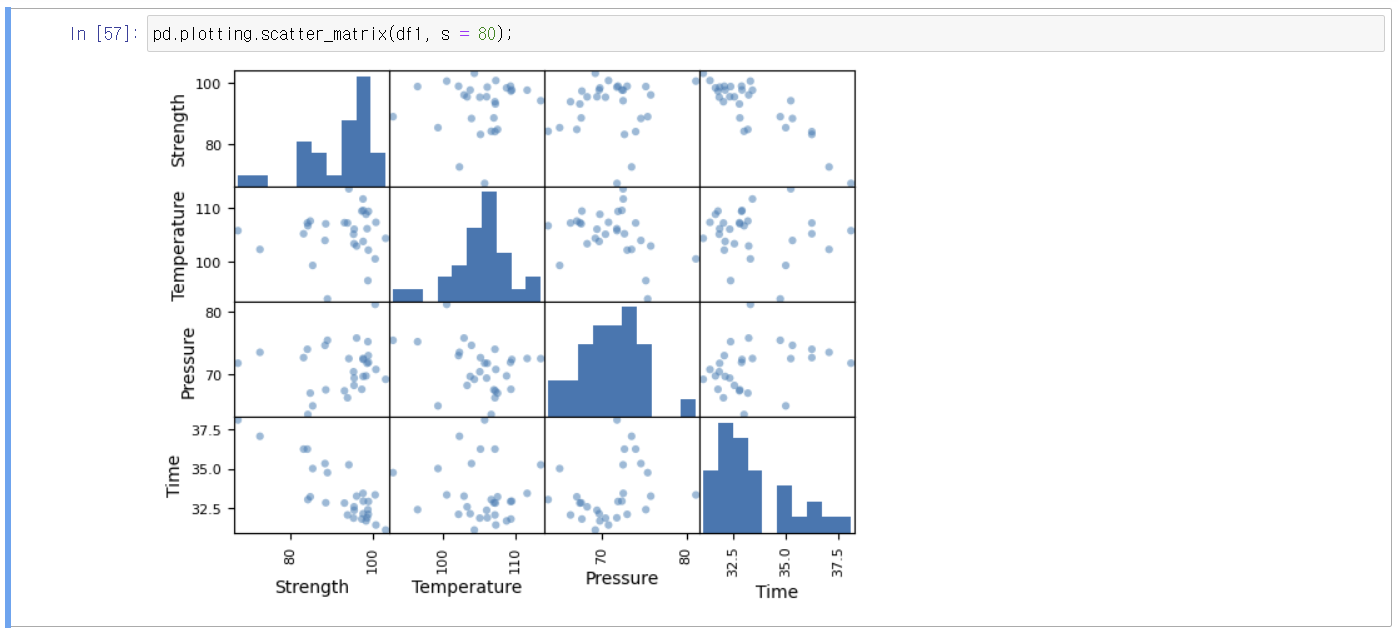
Time과 Strength가 corr가 있어 보임
시각적 분석은 주관적인 해석이 들어가다보니 corr을 구해볼 것
종속변수와 독립변수의 corr(둘 다 수치형이므로)

time만 상관계수가 높음(-0.8)
상관관계가 없다고 제거해버리면 안됨. interaction impact를 고려할 필요가 있으므로 함수로 제거해서는 안된다.
y와의 상관성이 있어보이는 변수는 time. x들끼리의 상관관계는 크게 있어보이지 않는다.
즉, 다중공선성 문제는 없어보인다. x들끼리 상관관계가 0.6 이상이면 심각할 수도 있다.
상관관계는 두 변수 사이의 관계만 고려하는 것이지만, vif(분산팽창지수)는 x1이 나머지 변수들과 얼마나 연결되어 있느냐를 확인하는 것임.
2) 독립성: 잔차가 설명변수와 독립적이다(상관이 없다). → 검증: 잔차산점도(X축: 적합값, Y축: 잔차), durbin-watson test
2-1) 잔차 산점도
m22.resid : 잔차(y축)
m22.fittedvalues : 적합값(x축)
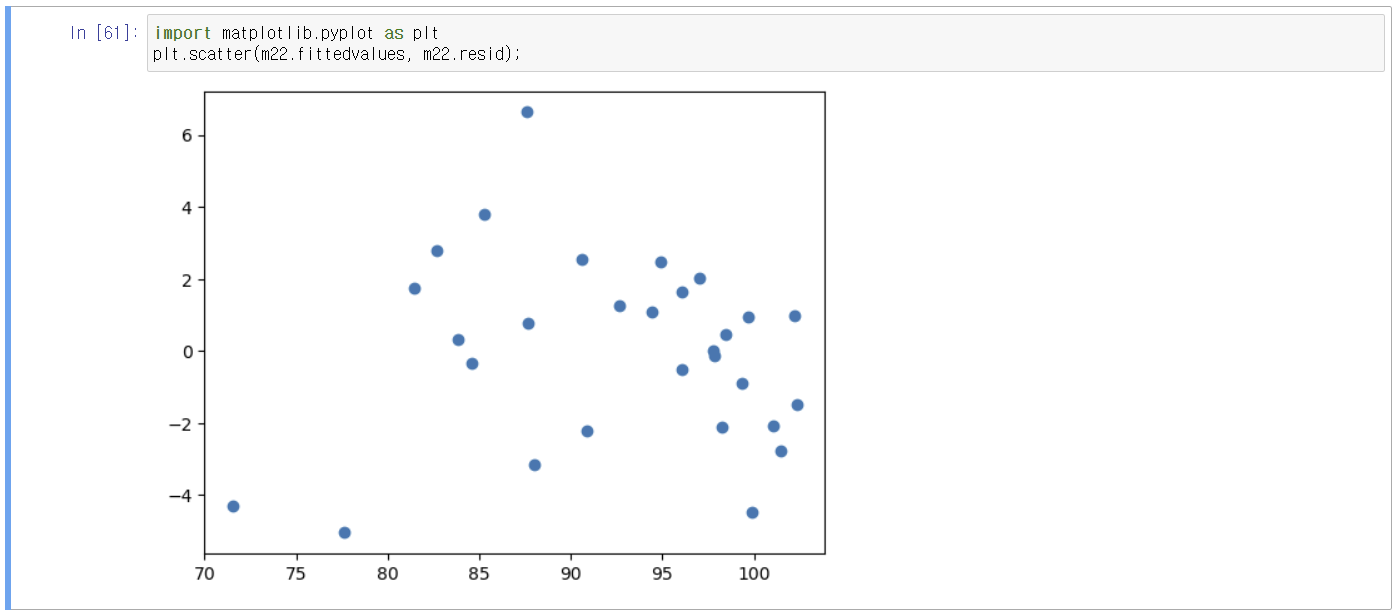
잔차 산점도의 별다른 패턴이 발견되지 않으므로 서로 독립적이다(주관적 판단)
객관적 분석을 수행하려면 더빈-왓슨 테스트를 하여야 함
2-2) durbin-watson test(durbin-watson 표로 기각 여부 결정) → durbin-watson 표가 신뢰구간(채택역) 제시함.
H0: 독립적이다.
H1: 독립적이지 않다.

더빗-왓슨 테스트에 잔차를 넣어주면 된다.
R에서 더빈 왓슨 테스트를 하면 p-value가 출력되나 파이썬에서는 p-value가 바로 출력되지 않으므로 더빈-왓슨 표를 찾아보고 확인하여햐 한다.
durbin-watson 표
https://real-statistics.com/statistics-tables/durbin-watson-table
alpha = 0.01은 잘 사용하지 않는다. 거의 채택역으로 출력된다(너무 긍정적인 결과만 나옴).
n은 샘플 사이즈, k는 독립변수 수.
→ 샘플사이즈(n)와 회귀모형 설명변수 수(k)를 적용하여 유의수준 0.05에서 신뢰구간: [1.198, 1.650]
따라서 검정통계량이 채택역 안에 있으므로 영가설 채택 → 독립적이라고 볼 수 있음.
3) 등분산성: 잔차의 분산이 일정하다(설명변수 변화에도)는 가정
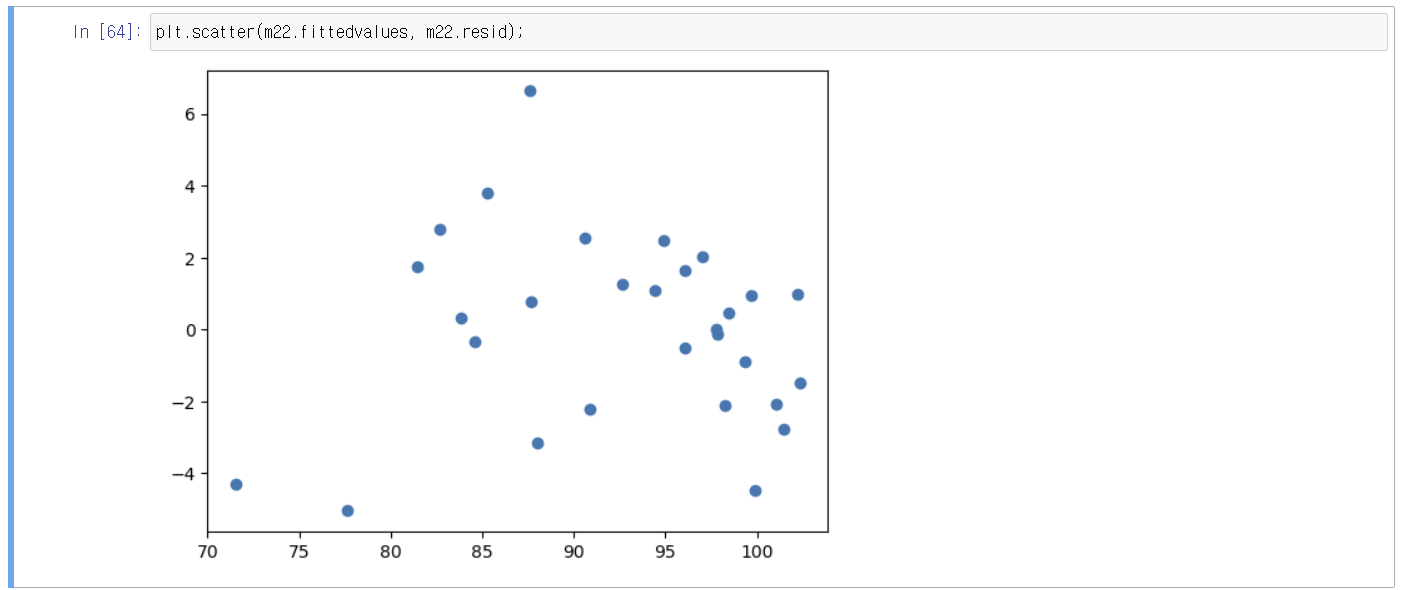
4) 정규성: 잔차가 정규분포를 따른다는 가정
4-1) 시각화 Q-Q plot, histogram, kde
일반 히스토그램
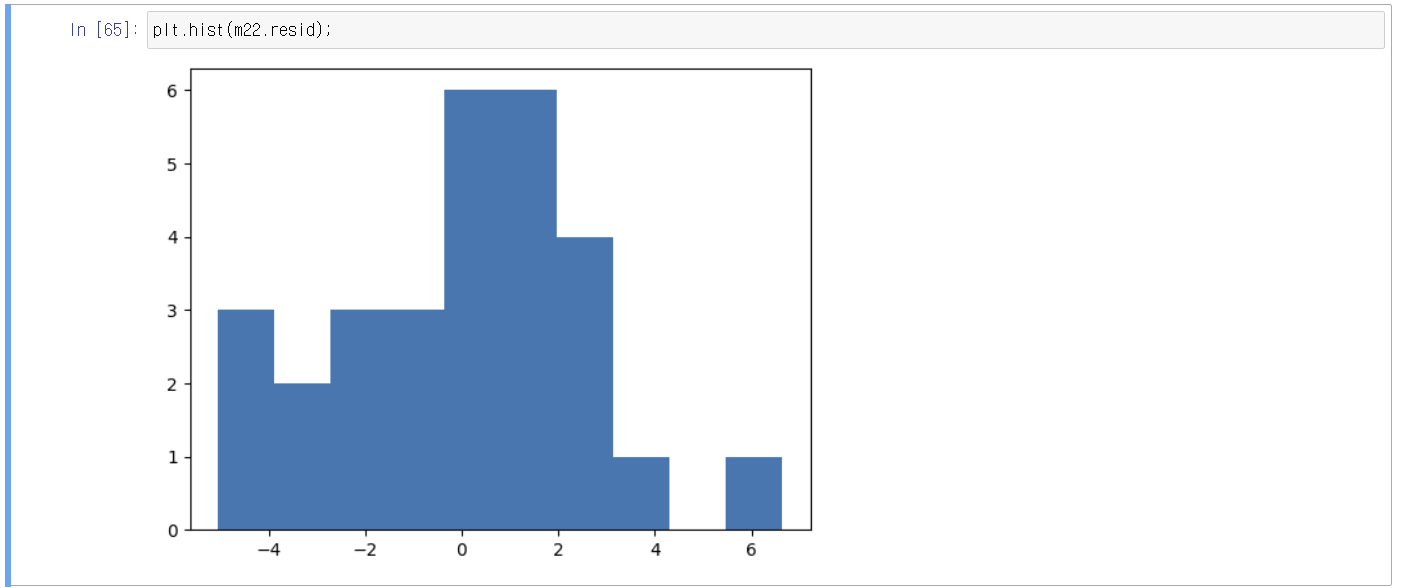
대략적인 분포를 봤을 때 정규분포와 유사한 분포를 보임
일반 히스토그램 + kde
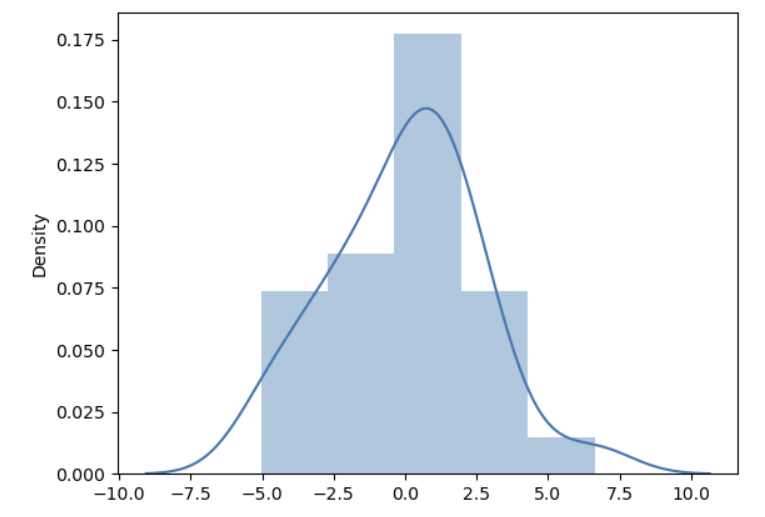
정규분포에 위배된다고 보기는 어렵다.
Q-Q plot
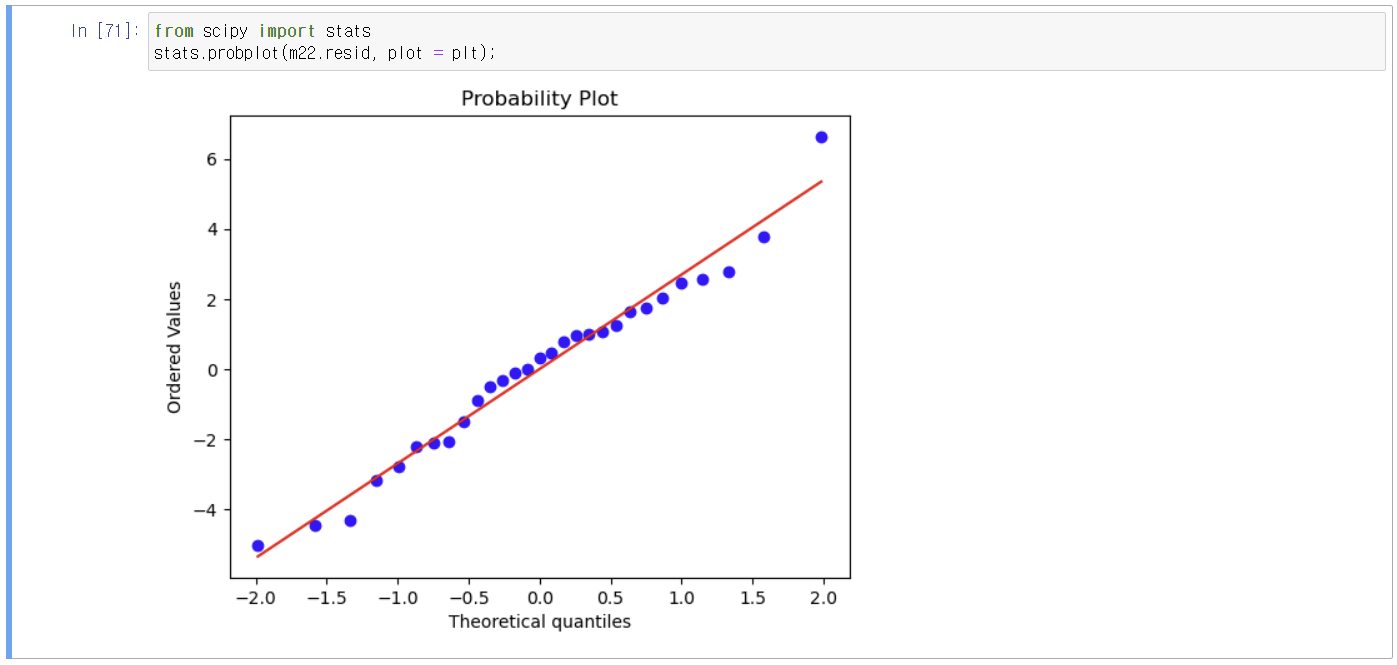
특별히 붉은 선에서 멀찍이 떨어져 보이는 값은 없다.
마지막 값은 떨어진 것으로 보이기는 하나 이상치 검증을 해 볼 필요가 있겠음.
주관적으로 봤을 때 크게 떨어져 보이지는 않기 때문이다.
이상치라고 판단이 되면 제거를 하도록 하겠다.
4-2) 가설 검정(샤피로윌크, K-S TEST)
샤피로윌크 검정
H0: 정규 분포를 따른다.

p-value가 0.05보다 크므로 영가설 채택 → 정규성 만족.
sample size가 2000 미만인 경우 샤피로윌크 검정, 2000이상일 경우 K-S TEST를 하는 것이 좋다.
8. 이상치 검정
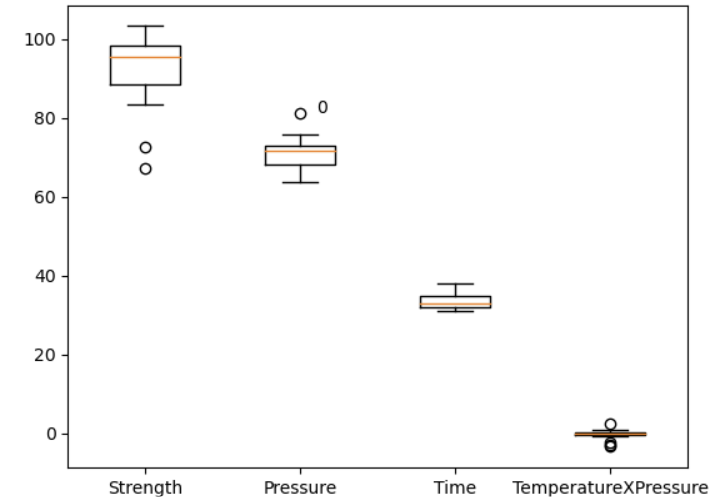
8-1) 모든 변수의 box plot
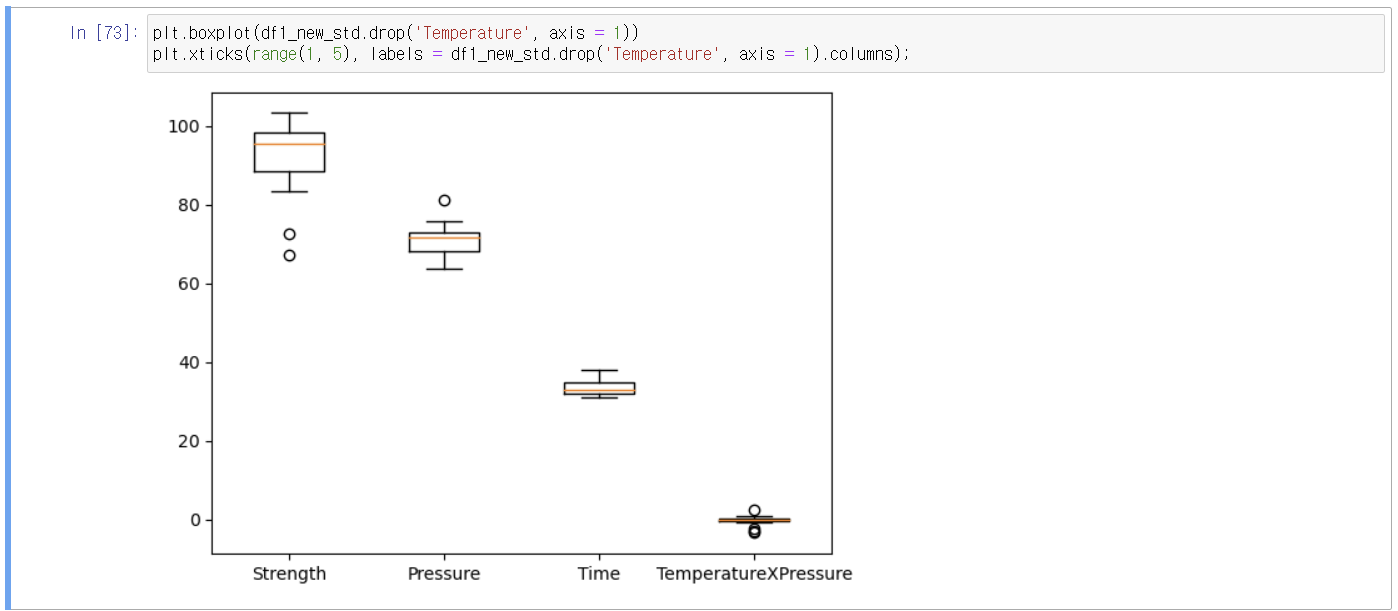
이상치 체크할 때
1) y값(회귀 같은 경우 일반적으로 y가 회귀선 근처에 있음. 회귀선과 떨어진 값이 있는지 확인) → 높거나 낮은 값에 대해서도 설명변수가 이를 잘 설명한다면 이상치라고 볼 수 없음
y끼리만 보는 게 아니라 잔차 boxplot을 보는 것이 좋음. 그래서 잔차가 큰 데이터들은 제거 하는 것이 좋음.
boxplot은 분포를 보는 것이므로 box를 넘어선 값을 이상치라고 바로 판단하기 어려울 수 있음
2) 각 x에 대한 분포
3) 전체 관측치(회귀식 입장에서는 잔차)에 대한 이상치 검정
이상치로 보이는 데이터 포인트에 행번호 부여하기

8-2) 잔차에 대한 box plot
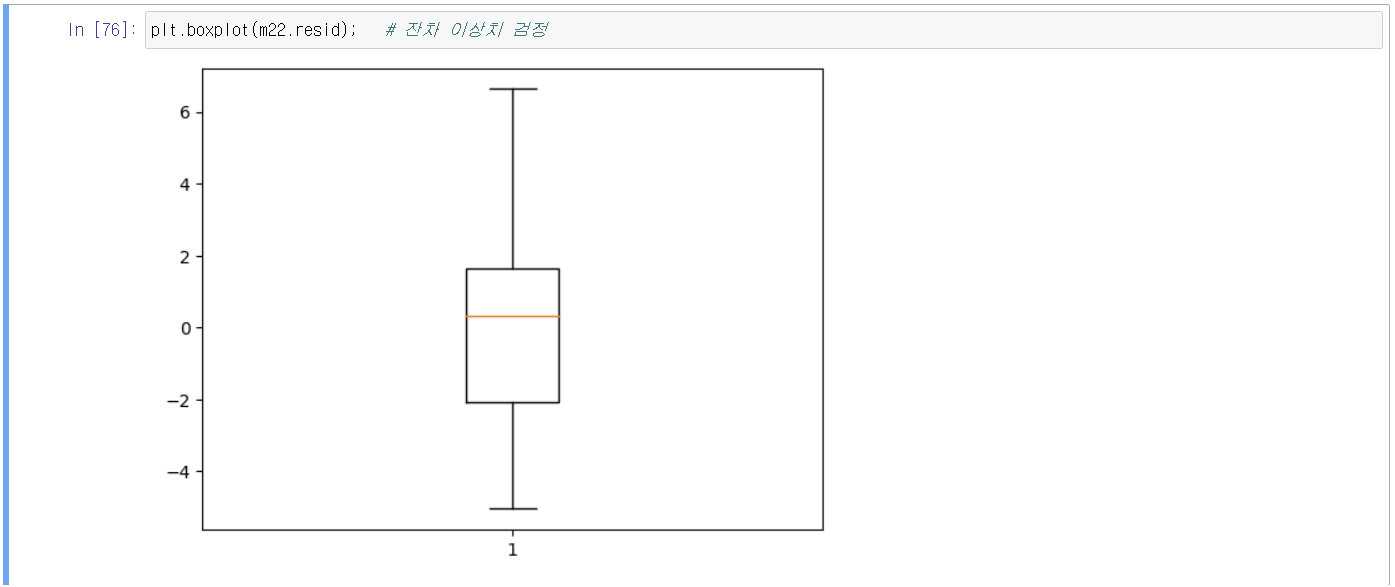
잔차 기준으로 boxplot 그렸으나 이상치는 보이지 않는다.
그래도 outlier test를 수행하여보겠다.
본페로니 p-value는 각각의 관측치들마다 동시에 outlier test를 하는 것이다.
관측치들끼리의 상관성이 있어서 신뢰하지 못하는 p-value가 출력되기도 하기 때문이다.
변수들 여러 개를 동시에 p-value를 수행할 때에는 일반 p-value보다는 본페로니 p-value를 진행하여야 한다.
Outlier Test
이상치 검정
H0: 이상치가 아니다.
H1: 이상치이다.
이상치 값 확인하기
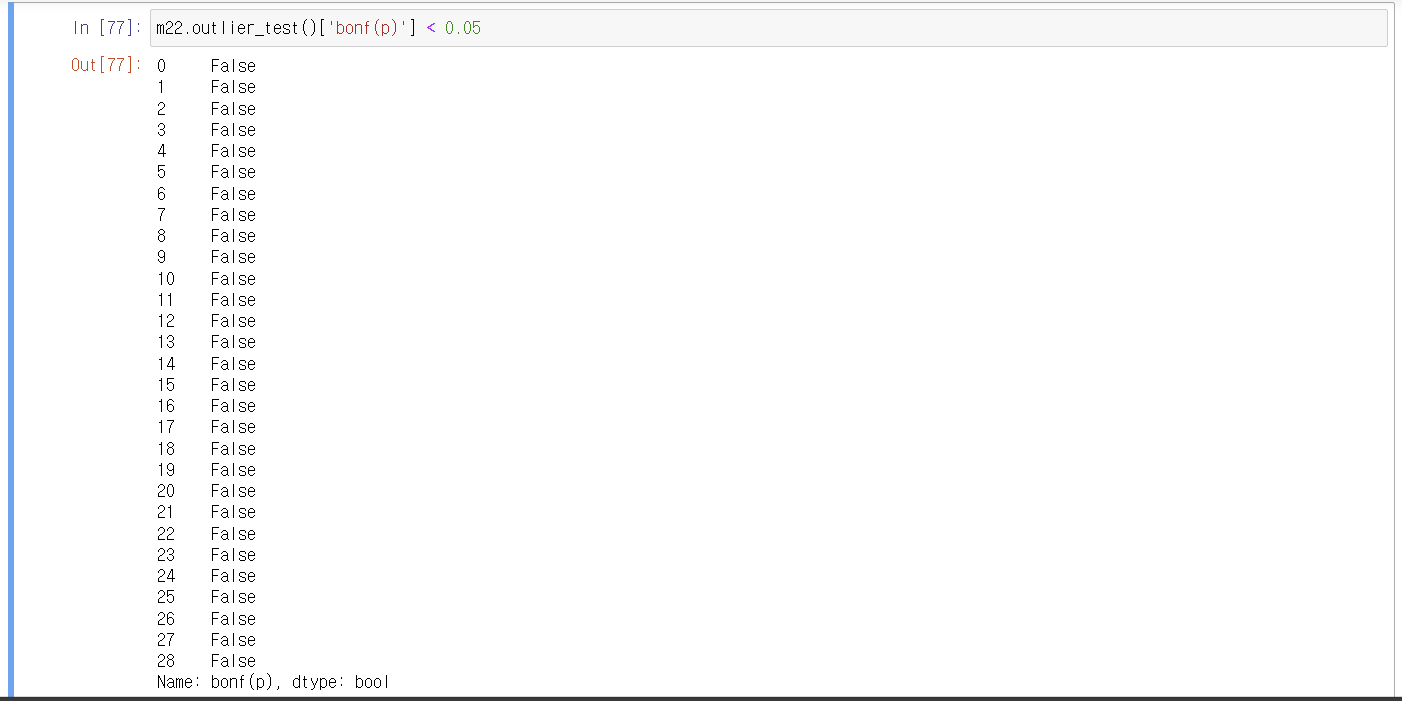
위에서 m22.outlier_test() 만 수행하면 표준화된 잔차, 수정되지 않는 p-value, 수정된 p-value(본페로니 p-value) 를 확인 할 수 있다.
본페로니 p-value를 봐야 각각 이상치를 검정한 결과와 같다고 볼 수 있다.
따라서 영가설 채택

이렇게 보면 null 출력되므로 이상치가 없는 것으로 판단된다.
** bonf(p) (bonferroni p-value): 한 번에 여러 가설에 대한 가설 검정 수행 시 각 관측치별로 재해석한 유의확률
9. 변수 변환
독립변수가 편포를 가질 때 주로 로그, 지수, 제곱, 역수 변환 시도

1) 로그 변환
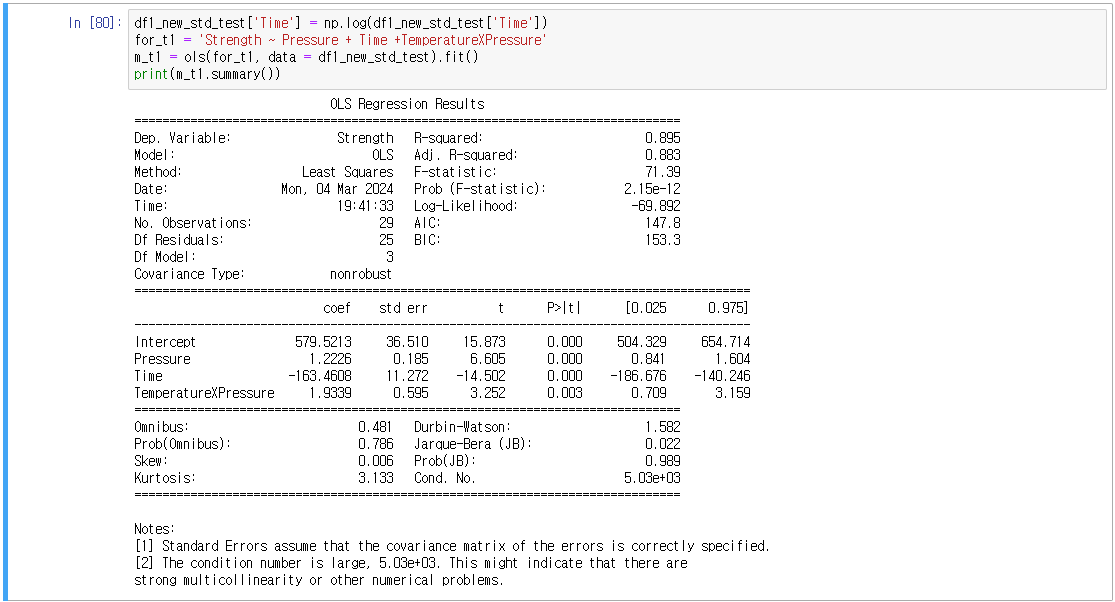
Time은 유효하나 R스퀘어 값은 낮아짐
2) 지수 변환
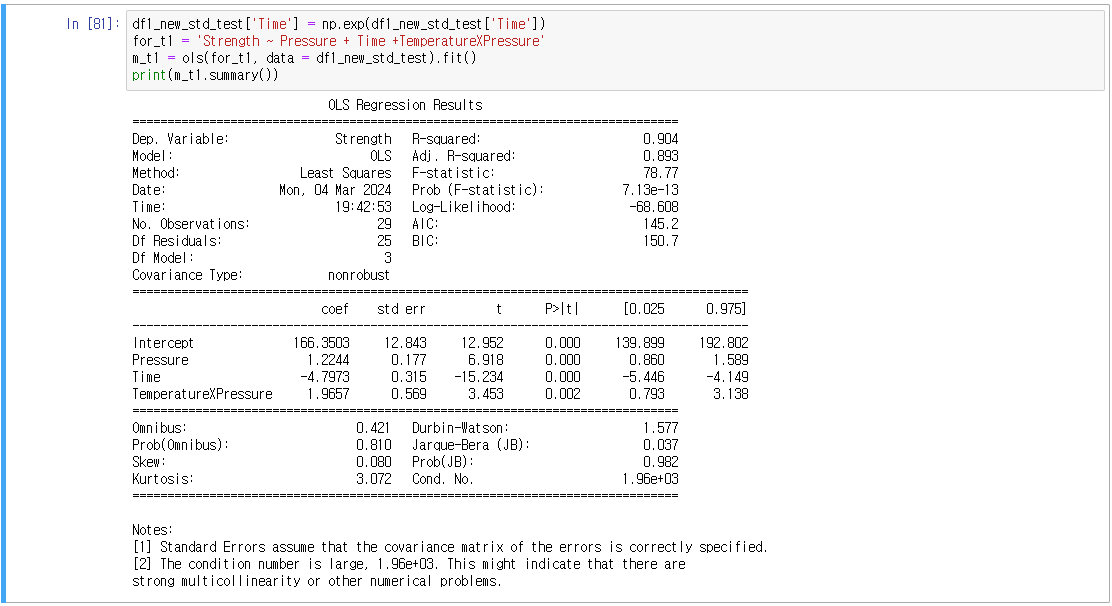
3) 제곱 변환

약 1점 오름.
정규분포 따르는지 궁금하여,
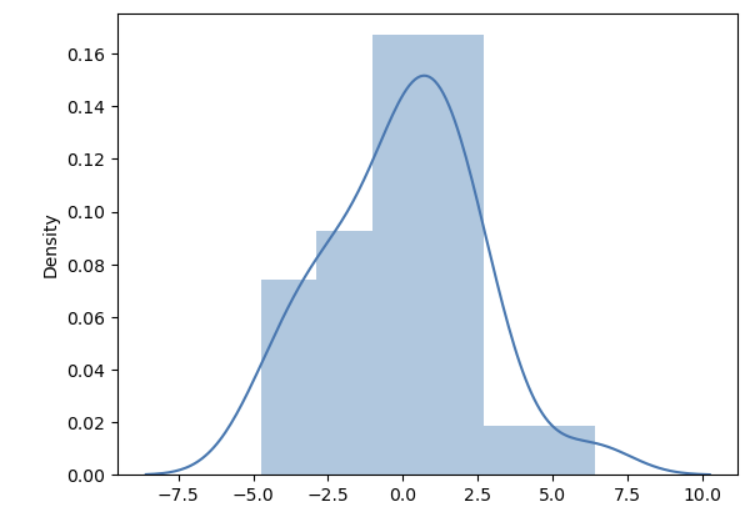
제곱변환하니 정규분포에 가까운 변화가 이루어지고 y값 예측에 도움이 되는 변수로 바뀌게 됨.
여기서 시사하는 바는, EDA를 꼼꼼히 하고 그것에 맞는 전략을 취하는 것이다.

샤피로 윌크 테스트를 해도 정규분포를 따른다고 나온다.
4) 역수 변환
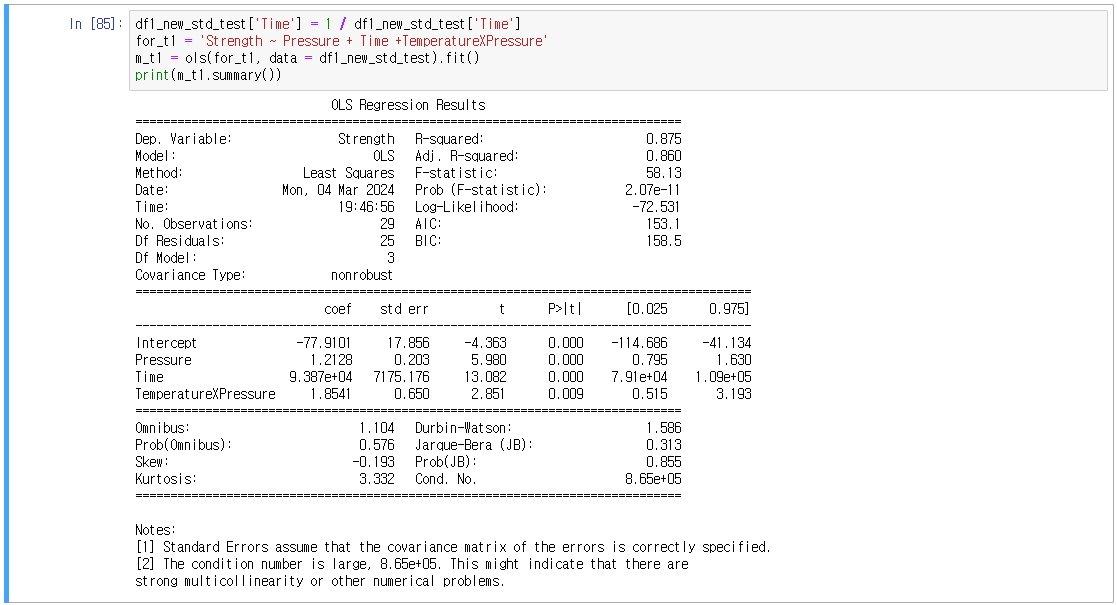
좋은 결과는 아님.
Time 변수를 적절하게 나타내는 것은 제곱 변환인 것으로 보인다.
제곱변환을 하면 기존의 편포가 어느 정도 해결이 되어 정규분포를 따르는 것처럼 보인다.
따라서 제곱변환에 의미가 있다.
'배우기 > 복습노트[Python과 분석]' 카테고리의 다른 글
| [복습] Python | 분석 | 군집분석(5) (0) | 2024.03.06 |
|---|---|
| [복습] Python | 분석 | 군집분석(2) (0) | 2024.03.05 |
| [복습] Python | 분석 | 연관분석(2) (0) | 2024.03.04 |
| [복습] Python | 분석 | 연관분석(1) + 하루끝(20240214) (0) | 2024.02.14 |
| [복습] Python | 분석 | 상호작용(=교호작용, interaction effect) + 하루끝(20240213) (0) | 2024.02.13 |



