차원축소(변수 결합으로 새로운 인공변수를 유도하는 방식)
1. 정의: 기존 변수들의 선형 결합으로 고차원 데이터를 저차원 데이터로 매핑(평탄화)
2. 활용: 시각화, 변수 결합, 차원축소(단순한 모델로 만들기 위한 방법 중 하나)
종류
1. PCA
- 기존 데이터가 가지고 있는 분산은 최대한 유지하면서 차원 축소
- 분산 설명력으로 차원에 대한 최종 결정(몇 차원으로 선정할 지 결정)
변수들에 가중치를 부여해서 결합하는 방식을 가중합(=선형결합)이라고 한다.
C1 = a1X1 + a2X2 + a3X3 + a4X4
이 때 기존 변수의 선형결합으로 차원을 축소하는 방법은 비지도학습이다. 변수의 변형이기 때문이다. 이에 따라 변수 스케일링도 비지도 학습이다. y가 불필요한 변수변환 기법이기 때문이다. 그래서 PCA를 대표적인 비지도 학습이라고 한다(MDS도 마찬가지로)
예) 수치 데이터(4차원 이상)들의 분류 분석 시 전체 데이터의 분포도 시각화
1. 데이터 로딩

2. 변수 스케일링
차원 축소를 할 때에는 계수를 추정하게 되는데, 계수의 크기가 중요하다. 변수 스케일이 다르면 계수에 영향을 줄 것이기 때문에 이를 막기 위하여 변수 스케일링이 사전에 수행되어야 한다.
(여기서는 분석 목적이 아니므로 train, test를 나를 필요가 없음)

3. 차원 축소 시도

위와 같이 계수는 8개 나와야 한다. 두 개의 주성분을 만들었으므로, 우리가 가지고 있는 변수가 4개니까 8개의 계수가 리턴되는 것이다.
C1 = a1X1 + a2X2 + a3X3 + a4X4
C2 = b1X1 + b2X2 + b3X3 + b4X4
즉, 인공변수 유도식은 다음과 같이 볼 수 있다.
C1 = 0.42494212*X1 -0.15074824*X2 + 0.61626702*X3 + 0.64568888*X4
C2 = 0.42320271*X1 +0.90396711*X2 -0.06038308*X3 -0.00983925*X4
위와 같은 수식을 만들어 주는 과정이 fitting, 수식에 train_x 값을 넣어 변환 시켜주는 것이 transform 과정이다.
분산 설명력

두 분산설명력의 합이 95%이므로 2차원으로의 축소가 의미가 있다.(기존의 데이터 분포와 꽤 유사하다고 불 수 있다).
두 번째 인공변수의 분산설명력이 첫 번째 인공변수의 분산설명력보다 낮은 이유는, 첫 번째 인공변수에서 주요 변동성을 다 설명했기 때문이다.
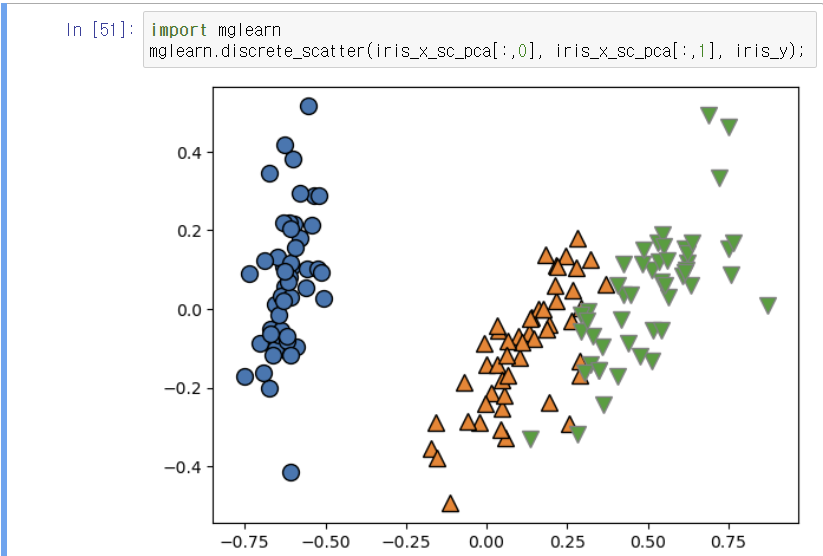
2차원 시각화
인공변수 수에 따른 분산 설명력 확인


3차원으로 나타내보기

3차원 시각화

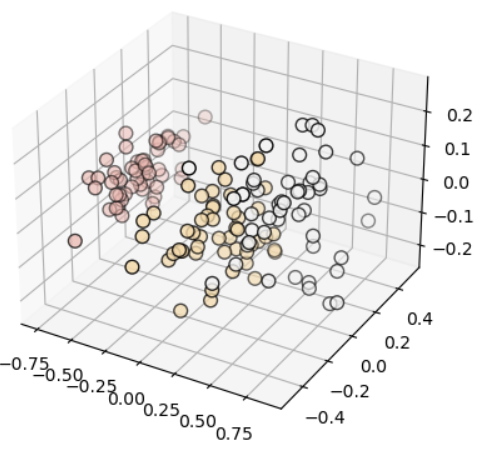
참고 - scatter 색상 지정


2. MDS
- 기존 데이터가 갖는 거리는 최대한 유지하면서 차원 축소
- stress: 기존 데이터포인트들끼리의 거리의 총 합과, 유도된 인공변수로 인한 데이터포인트들의 거리의 차이
(이 값이 작을 수록 raw data의 특성을 그대로 유지함을 의미)
- stress로 차원에 대한 최종 결정
모든 데이터포인트들끼리의 거리를 다 계산해서, 기존 데이터포인트들끼리 가지고 있는 거리의 총합에 대해, 차원 축소 후 얼마만큼 거리를 잃었는 가에 대한 것이 stress 이다.
분산 설명력의 경우, 설명변수가 많아질수록 원본가 가까워지기 때문에 당연히 설명변수가 많아질수록 분산설명력이 커진다. 그러므로 elbow point를 찾아 급변하는 지점을 찾는 것이 중요하다(그래프 우상향).
그러나 stress는 반대로, 설명변수가 증가하면 본래 변수와 같아지므로 stress는 줄어든다. 이 때에도 stress가 급변하느 지점의 설명변수 수를 찾으면 되겠다(그래프 우하향).
stress는 학자들마다 주장하는 종류가 다양한데, 그 중 유명한 거리는 kruskal stress 이다.
예) 수치데이터(4차원 이상)들의 분류 분석 시 전체 데이터의 분포도를 시각화 하여라(MDS로 차원 축소)
1. 데이터 로딩

2. 변수 스케일링

3. 차원 축소 시도

4. stress 확인

kruskal stress가 아닌 이상 절대적 기준은 없다.
분산 설명력의 경우 80 이상이라는 절대 기준이 있는데, stree가 18이라고 했을 때 그게 좋은지 알 수가 없다는 의미이다.
즉 sklearn에서 제공하는 stress는 절대적 해석 기준이 없다.
그러므로 인공변수 수의 변화에 따른 stress 변화를 확인하여 적절한 인공변수 수를 결정하여야 한다.

시각화

4. 차원 축소 결과 시각화(산점도)
2차원

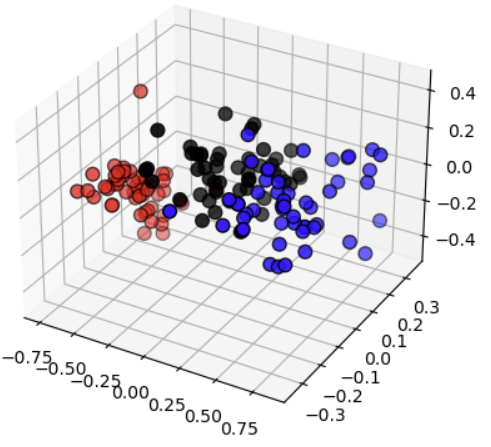
3차원

5. kruskal stress 계산
- 절대적 기준 존재
- < 0.025 완벽
< 0.05 매우 좋음
< 0.1 좋음
< 0.2 보통
>= 나쁨
ss^2 = sum((DA - DE)^2) / sum(DA^2)
ss = sqrt( sum((DA - DE)^2) / sum(DA^2) )
DA(실제거리): 차원 축소 전 데이터포인트들간의 거리
DE(예상거리): 차원 축소 후 데이터포인트들간의 거리
직접 계산

'배우기 > 복습노트[Python과 분석]' 카테고리의 다른 글
| [복습] Python | 분석 | knn(거리기반 모델) (0) | 2024.02.11 |
|---|---|
| [복습] Python | 분석 | 차원축소(PCA, MDS) (2) (0) | 2024.02.10 |
| [복습] Python | 분석 | SVM(Support Vector Machine) (4) (암의 양성 여부 예측) (0) | 2024.02.09 |
| [복습] Python | 분석 | 스케일링(scaling) + 하루끝(20240201) (0) | 2024.02.08 |
| [복습] Python | 분석 | SVM(Support Vector Machine) (3) (0) | 2024.02.08 |



