지난 시간에 이어 시각화를 계속 학습하였다.
내일 시각화가 마무리 될 예정이다.
이제까지 배운 내용에 대한 복습 겸 오늘 배운 내용을 쭉 나열해보도록 하겠다.
설명이 없는 것은 지난 링크를 확인하면 되겠다.
https://metime.tistory.com/169
[복습] R(programming language) 시각화(1)(선그래프) + 하루끝(20231208)
시각화에는 기본 시각화 함수와 ggplot2 패키지가 있다. 우선 기본 시각화 함수로 여러 그래프를 출력해보도록 하겠다. 1. 선 그래프(산점도): 분포를 확인하거나 x축과 y축의 상관관계를 시각화하
metime.tistory.com
https://metime.tistory.com/172
[복습] R(programming language) 시각화(2) (barplot, pie, pie3D) + 하루끝(20231211)
https://metime.tistory.com/169 [복습] R(programming language) 시각화(1)(선그래프) + 하루끝(20231208) 시각화에는 기본 시각화 함수와 ggplot2 패키지가 있다. 우선 기본 시각화 함수로 여러 그래프를 출력해보도
metime.tistory.com
시각화
1. 산점도: plot
2. 선그래프: plot(type = 'o'), lines
3. 파이차트: pie, plotrix::pie3D
4. 상자그림: boxplot
- 연속형 자료의 분포 파악 및 비교
- 이상치 검증에도 사용됨
boxplot을 하나 생성해보자.



이상치가 위와 같이 표현되기 때문이다.
분석에 대해서는 나중에 자세히 배우게 될 것이고 우선 간단히만 설명해주셨다.
IQR 지표는 Q3-Q1으로, IQR이 클수록 분포가 크다.
이상치 중에서 위에 있는 이상치는 상한 이상치로, Q3+1.5*IQR보다 크면 상한 이상치라고 하며,
하한 이상치는 Q1-1.5*IQR보다 작을 경우 하한 이상치라고 한다.
이 식으로 이상치 검정을 하는 것이다.
bar plot은 최솟값, 최댓값, 중간값, 이상치의 정보를 알 수 있으나 평균이나 분산은 알 수 없다.
수염의 길이는 이상치를 제외한 최솟값과 이상치를 제외한 최댓값의 크기이다.
관련 예제를 풀어보겠다.
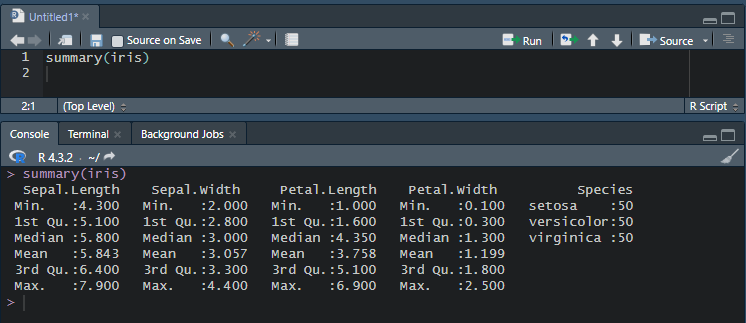
iris의 두 번째 컬럼(sepal.width)에서 box plot 기준 이상치를 찾고 이상치들의 sepal.width의 평균을 출력하여라.
summary(iris)하면 iris의 통계정보가 출력된다. 이 정보를 바탕으로 계산하면 되겠다.
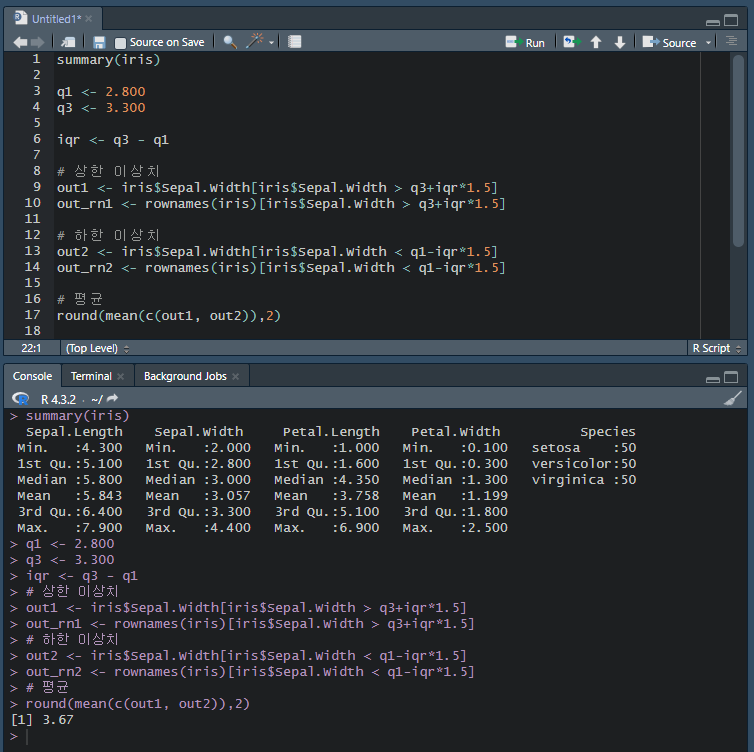
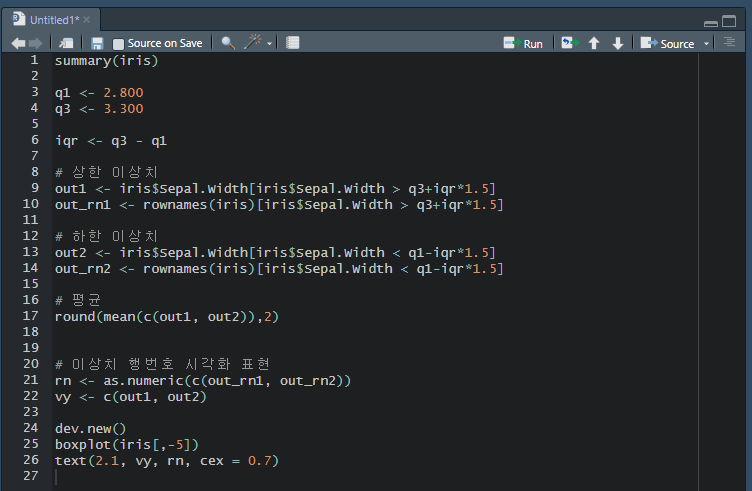
위의 값에 대하여 이상치 행 번호를 시각화 하여라.

5. 히스토그램: hist
- 연속형 그래프의 분포를 파악하기 위한 용도의 시각화 기법으로, 도수분포표를 직사각형 형태로 시각화한다.
- 막대가 서로 붙어 있으며 막대의 폭(=계급의 크기)은 일정하여야 한다. 막대의 수 또는 계급의 크기는 조절이 가능하지만 반드시 전체 막대의 폭은 일정해야 한다.
- 이상치 검정에 사용되기도 한다. 특정 계급의 빈도가 낮은데 다른 중심과 동떨어져 표현되어 있다면 이를 중점적으로 볼 필요가 있기 때문이다.
옵션은 아래와 같다.
hist(x, # 벡터
breaks, # 계급의 구간 정의
prob = F, # y 축 좌표 확률표현 여부
includ.lowest = T, # 첫 번째 계급에 최솟값 포함 여부(새로운 계급을 열지 말고)
right = T, # right closed 여부
...)
히스토그램을 출력해보자.



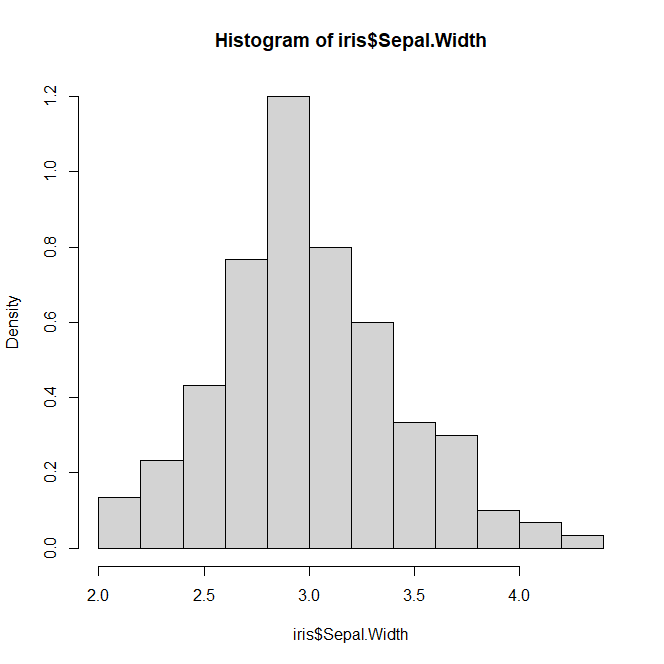
prob 옵션을 TRUE로 설정하면 y축은 Density가 된다.
다음 벡터의 분포를 히스토그램으로 표현해보자.


현재 위 그래프는 right=T가 default 이므로 right closed 형태이다.
right closed란 140~150범위의 경우 140초과 150이하 라는 의미이며
right=F 옵션으로 설정하는 경우 140이상 150미만으로 그래프가 그려진다.
140초과 150이하인데 벡터 값을 보면 해당 범위에 속하는 값은 두 개인데 그래프에는 3개로 되어있다.
이는 includ.loewst=T가 default이기 때문이며, 이 의미는 첫 번째 계급에 최솟값을 포함하겠다는 의미이다. 그래서 130~140이라는 새로운 계급이 그래프에서 열리지 않은 것이다.
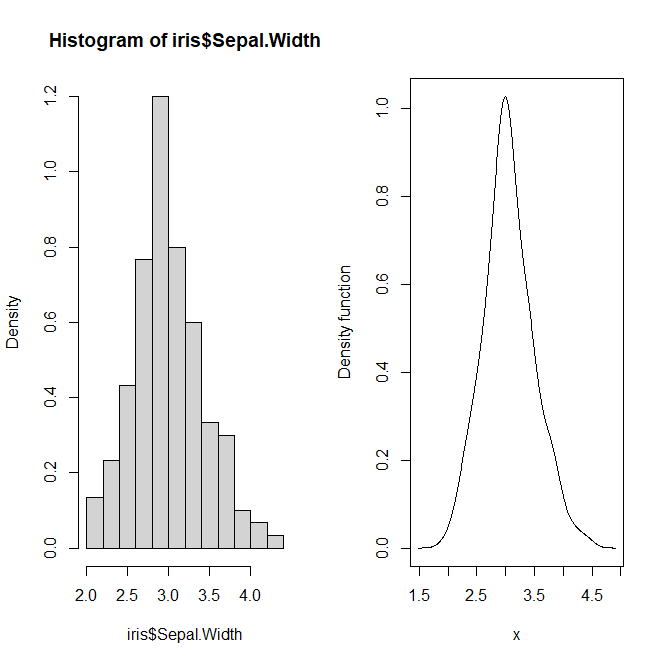
6. kde(커널 밀도 함수)
- 연속형 테이터 분포를 파악하는 데에 사용되며, 히스토그램과 유사하나 히스토그램의 계급을 잘게 쪼개어 이은선 그래프로 나타낸 형식이다.
kde는 패키지를 설치하여야한다.
install.packages('ks')
library(ks)

다음은 시각화 옵션이다.
이 부분 역시 따로 설명이 없는 부분은 지난 시간 자료를 참고하면 된다. 위의 링크에 있다.
1.범례설정: legend
2. 눈금: axis
3. 텍스트: text
4. 제목: title
5. 화살표: arrows
6. 여백: par(mar)
7. 사각형: rect


8. 채우기: polygon
polygon(x,
y,
...)
유용하게 쓰이는 함수이다.
먼저 네모를 그려보자.

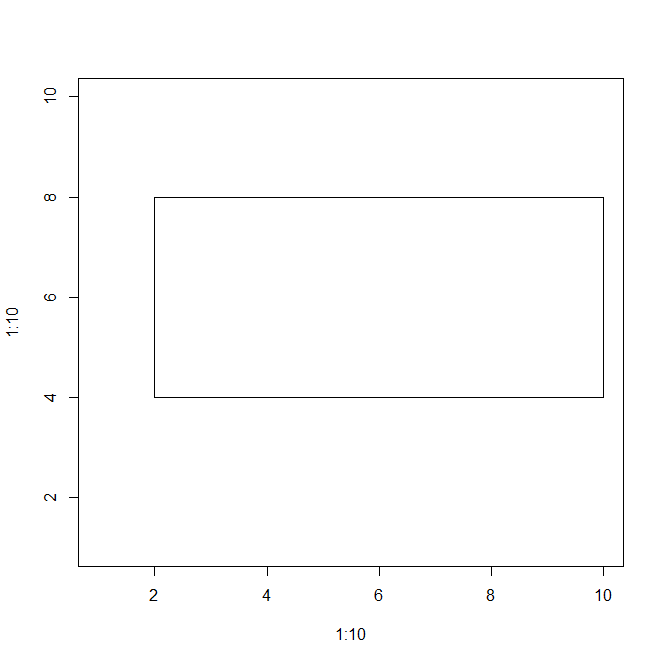
위 코드에서 점의 위치를 바꾸어 나비넥타이 모양을 만들고 빨간색 빗금을 칠하여보자.


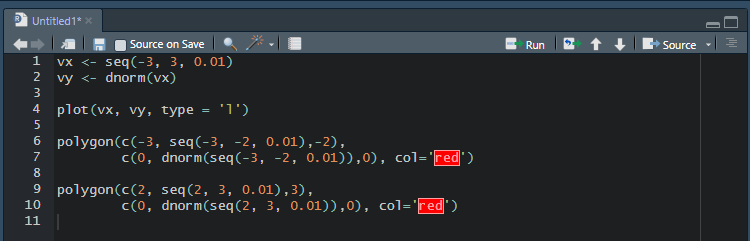
polygon이 중요한 이유는 나중에 정규분포를 그리고 가설검증을 할 때 기각역과 채택역을 설정하게 되는데, 영가설을 기각할 수 있는 영역과 채택할 수 있는 영역을 그래프상에서 칠하게 된다. 이 때 필요한 함수이다.
0을 중심으로 -3과 3 사이의 표준정규분포 곡선을 그리고 -2와 2를 기준으로 그래프 양측 영역을 칠하여보자.

외부패키지를 사용한 시각화
install.packages('ggplot2')
library(ggplot2)
ggplot2 패키지를 사용한 시각화이다.
1. 기본 구성
- ggplot: 데이터, 변수 정의
- aes:변수 정의
2. 시각화 함수
- geom_line: 선그래프
- geom_bar : 막대 그래프
- geom_point : 산점도
- geom_boxplot: 박스그래프
- geom_histogram: 히스토그램
3. 옵션함수
- xlab, ylab, xlim, ylim, ggtitle, theme, geom_text, facet_grid
산점도를 먼저 살펴보자.
ggplot(data = .
mapping = aes().
...)
예제) iris$Sepal.Length, iris$Sepal.Width 산점도 그리기

Line 2뒤에 +를 붙임으로써 그림을 계속 덧그리고 수정할 수 있어서 확장성에 용이하다.
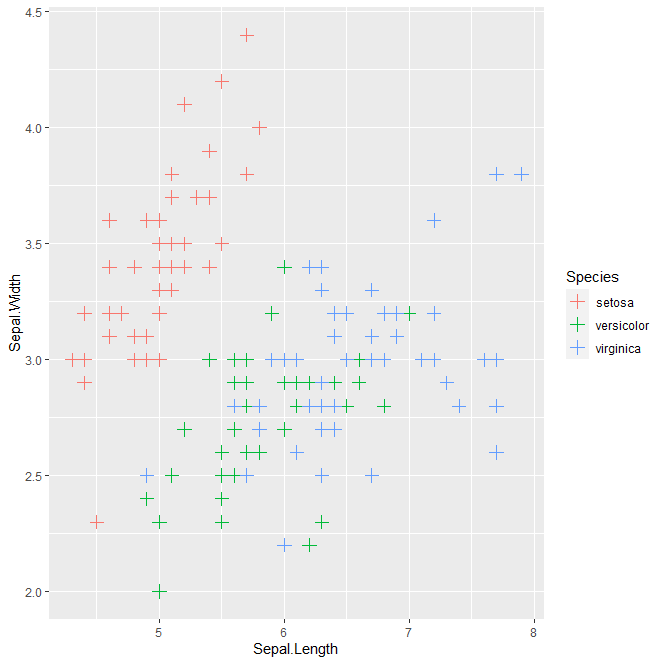
legend도 자동생성해준다.
이 때에 factor 처리의 경우, Species가 만일 factor가 아니어도 Species별로 컬러 표시를 해준다.
aes의 데이터에서 정보를 가져오기 때문이다.
사용자 정의 팔레트 전달 산점도를 살펴보자.
iris의 경우 150개의 건수마다 색을 정의할 필요가 없다.
컬러에 이름을 전달하여 factor의 값이 다를 때, 즉 클래스끼리 서로 다른 색 표현을 전달하라는 의미를 가지므로 3개의 컬러만 가지고 있으면 된다.
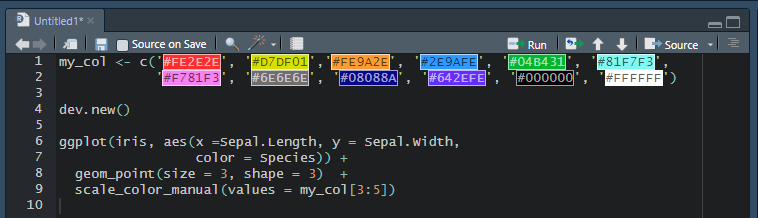

사용자 정의 컬러를 전달할 때,
scale_color_manual, scale_fill_manual이 있는데
scale_color_manual는 선 그래프,
scale_fill_manual는 막대그래프, 히스토그램 처럼 막대의 색을 채울 때 사용한다.
연습문제를 풀어보자.
cancer.csv 파일을 읽고 radius_mean 과 texture_mean의 ggplot을 출력하여라.

위와 같이 세 가지 case로 출력할 수 있다.
Line 10은 기존 plot함수로 그렸으며, dignosis가 factor로 되어있지 않기 때문에 Line11처럼 factor로 지정해 준 후 추후에 색을 입혀 출력한다. 색은 ifelse로 지정해주어 모든 데이터 포인트를 동시에 시각화 하는 방법으로 나타낸 것이다.
Line 18의 경우는, points 함수를 사용하여 그렸으며, 데이터 포인트 집단끼리 각각 시각화 하는 방법으로 풀이한 코드이다.
위 둘의 결과는 다음과 같이 출력된다.

마지막으로 Line29의 경우에는 ggplot을 사용하여 나타낸 것으로 결과는 아래와 같다.

다음은 ggplot으로 그리는 선 그래프이다.
ggplot2 패키지 사용 시 long data 전달이 가능하다.
또한 특정 컬럼의 class 별로 서로 다른 선 그래프 출력이 가능하다.
여러 선 그래프를 출력해보자.
1) 단일 선 그래프(선만 시각화)



이렇게 변수 지정하여 출력 또한 가능하다.

2) 단일 선그래프(점과 같이 시각화)

위의 g1 결과에 geom_point를 추가하여 시각화하였다.

3) 서로 다른 선 그래프

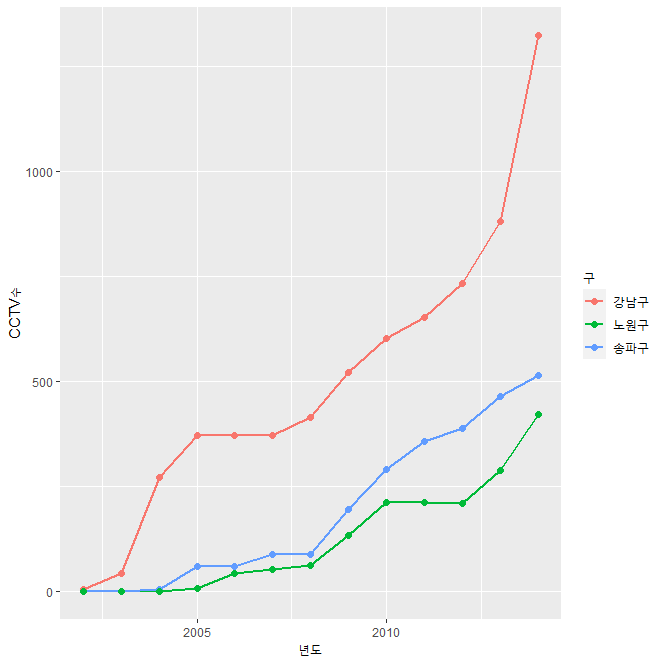
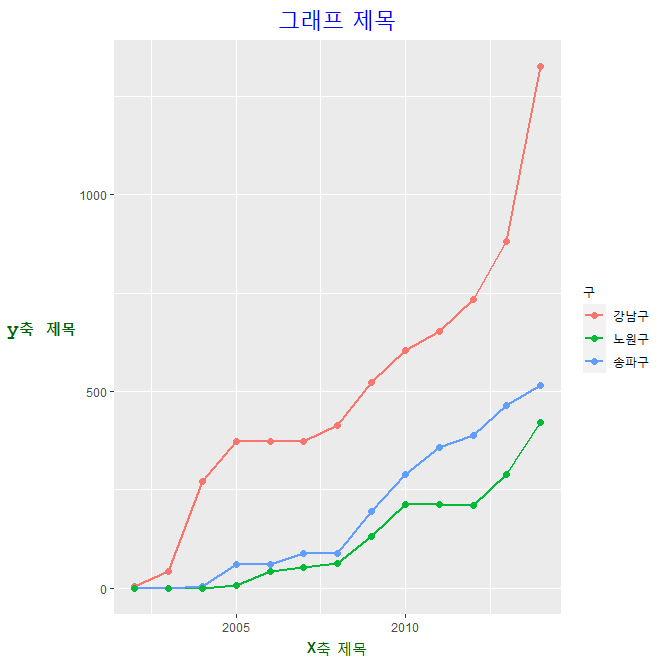
위 그래프에 시각화 옵션을 주면 다음과 같다.

'배우기 > 복습노트[R과 분석]' 카테고리의 다른 글
| [복습] R(programming language) 시각화(4) (ggplot2를 이용한 산점도, 선그래프, 막대그래프, 상자그림, 히스토그램, 확률밀도함수(KDE) 및 여러 옵션) (0) | 2023.12.13 |
|---|---|
| [실습문제] 2023. 12. 12.(화) (2문제) (0) | 2023.12.13 |
| [실습문제] 2023. 12. 11.(월) (2문제) (0) | 2023.12.12 |
| [복습] R(programming language) 시각화(2) (barplot, pie, pie3D) + 하루끝(20231211) (0) | 2023.12.11 |
| [실습문제] 2023. 12. 8.(금) (2문제) (0) | 2023.12.11 |



